সমপ্রান্তিক উপযোগ বিধি বা ব্যয়িত প্রতি টাকার উপযোগ কাকে বলে

সমপ্রান্তিক উপযোগ বিধি বা ব্যয়িত প্রতি টাকার উপযোগ এবং ভোক্তার ভারসাম্য

 Law of Equi-marginal Utility or Utility per Taka Spent and Consumer Equibrium

মার্শালের উপযোগ বিশ্লেষণে সমপ্রান্তিক উপযোগ বিধি একটি গুরুত্বপূর্ণ ধারণা।

ভোক্তার আয় সীমিত। আরও নিখুঁতভাবে বললে ভোক্তার ব্যয়যোগ্য আয় সীমিত। তাই প্রত্যেক ভোগকারী তার সীমিত আয়ের মধ্যে থেকে সর্বাধিক উপযোগ লাভ করতে চায়। অর্থাৎ সীমিত আয়কে ভোগকারী বিভিন্ন দ্রব্য ক্রয়ের জন্য এমনভাবে ব্যয় করে যাতে তার সর্বাধিক উপযোগ লাভ হয়।

একটা উদাহরণ দিয়ে ব্যাখ্যা করছি।

ধরি, আজিম মাছ বাজারে গেল। সে মাছ বাজারে ঢুকল। এক সপ্তাহের জন্য মাছ কিনবে। তার সব চেয়ে প্রিয় মাছ ইলিশ এবং সব চেয়ে কম প্রিয় মাছ চাষ করা পাঙ্গাশ। অর্থাৎ, আজিম সবচেয়ে বেশি উপযোগ লাভ করে ইলিশ মাছ  থেকে এবং সব চেয়ে কম উপযোগ লাভ করে চাষ করা পাঙ্গাশ মাছ থেকে।

আজিম কি পুরা এক সপ্তাহের জন্য সব ইলিশ কিনবে?

ইলিশের দাম যেহেতু সব চেয়ে বেশি সে সব ইলিশ মাছ কিনবে না।

যেহেতু তার ব্যয়যোগ্য আয় সীমিত, তাই সে ইলিশ এবং অন্যান্য মাছ এমনকি চাষের পাঙ্গাশ মাছও কিনবে।

সব মাছ একই পরিমান কিনবে? নিশ্চয়ই তাও নয়।

সে তার মাছ কেনার বাজেটকে এমনভাবে ভাগ করবে যে সে বিভিন্ন মাছ ভিন্ন ভিন্ন পরিমানে কিনে তার এক সপ্তাহের মাছের অভাব পূরণ করতে পারে।

অনুরূপভাবে মানুষ তার ব্যয়যোগ্য আয় দিয়ে বিভিন্ন দ্রব্য ও সেবা ক্রয় করে সর্বোচ্চ উপযোগ প্রাপ্তির চেষ্টা করে।

ভোগকারীর এই সর্বাধিক তৃপ্তি লাভের অবস্থা তথা ভারসাম্য অবস্থা নির্ধারণের জন্য অধ্যাপক মার্শাল সমপ্রান্তিক উপযোগ বিধি ধারণাটি প্রদান করেন।

ভোগকারী তার যুক্তিসিদ্ধ আচরণ দ্বারা নির্ধারণ করে কোন দ্রব্য কতটুকু ক্রয় করবে।

অর্থাৎ, ভোগকারী তার আচরণের দ্বারা বিভিন্ন দ্রব্যের পরিমানের মধ্যে পরিবর্তন এনে বিচার বিশ্লেষণ করে যাতে তার   মোট উপযোগ সর্বাধিক হয়।

সমপ্রান্তিক উপযোগ বিধির অনুমিত শর্ত

1. ভোক্তা বিবেকবান। অর্থাৎ, ভোক্তার আচরণ যুক্তিশীল।
2. ভোক্তার আয় সীমিত।
3. কোন নির্দিষ্ট সময়ে ভোক্তার অভাব স্থির।
4. দ্রব্যের দাম নির্ধারিত এবং বিভিন্ন দ্রব্যের দাম সম্পর্কে ভোক্তা সচেতন।
5. নির্দিষ্ট আয়কে প্রয়োজন অনুসারে বিভিন্ন পণ্য ক্রয়ে বন্টন সম্ভব।

সমপ্রান্তিক উপযোগ বিধি বিশ্লেষণ

কোন দ্রব্যর প্রান্তিক উপযোগকে সে দ্রব্যের দাম দ্বারা ভাগ করলে ব্যয়িত অর্থের প্রান্তিক উপযোগ পাওয়া যায়।

মার্শালের মতে, ভোক্তা তার সীমিত আয় বিভিন্ন দ্রব্য ক্রয়ে এমনভাবে ব্যয় করে যাতে প্রতিক্ষেত্রে অর্থের প্রান্তিক উপযোগ অর্থাৎ উপযোগ ও দামের অনুপাত সমান হয়।

এ সমতাস্থলেই নির্ধারিত হয় ভোক্তার সর্বাধিক উপযোগ তথা ভারসাম্য অবস্থা।

মনে করি, ভোগকারী X ও Y দুটি দ্রব্য ক্রয় করে। এদের মূল্য যথাক্রমে Px ও Py, ভোক্তার আয় M এবং অর্থের প্রান্তিক উপযোগ MUm = λ ।

এখন ভোক্তার উপযোগ সর্বোচ্চকরণের ভারসাম্য শর্ত নিম্নোক্তভাবে প্রকাশ করা যায়।

Mux / Px = MUy / Py = λ.

তালিকা/সূচি দ্বারা সমপ্রান্তিক উপযোগ বিধি বিশ্লেষণ

ভোক্তা যে দুটি দ্রব্য X ও Y ক্রয় করে নিম্নে সূচি / তালিকার সাহায্যে সে দ্রব্য দুটির প্রান্তিক উপযোগ এবং প্রান্তিক উপযোগ ÷ দাম দেখানো হয়েছে।

ধরি, Px = 5 এবং Py = 4, λ = 4 ইউটিল।

তালিকাঃ X ও Y দ্রব্যের বিভিন্ন এককের প্রান্তিক উপযোগ ও দামের অনুপাত

উপরের তালিকা হতে দেখা যায় যে, প্রতিটি দ্রব্যের অতিরিক্ত একক ক্রয়ের সাথে প্রান্তিক উপযোগ ও দামের অনুপাত ক্রমশ হ্রাস পায়।

এখন, MUx/Px = MUy/Py শর্তানুসারে ভোক্তা 2 একক X দ্রব্য এবং 3 একক Y দ্রব্য ক্রয় করলে তার সর্বাধিক উপযোগ লাভ ঘটবে। অর্থাৎ সে ভারসাম্য অবস্থায় পৌঁছাবে। কারণ, 2 একক  X দ্রব্য এবং 3 একক Y দ্রব্য ক্রয় করলে  MUx/Px = MUy/Py = 4 হবে। ভারসাম্যের শর্ত MUx/Px = MUy/Py = λ এক্ষেত্রে সর্বদাই 4 ইউটিলের সমান হবে।

আচ্ছা, বুঝতে কঠিন মনে হলে আমরা একটু সহজভাবে বুঝার চেষ্টা করি।

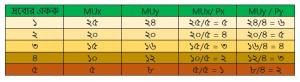
X ও Y দ্রব্যের বিভিন্ন এককের প্রান্তিক উপযোগ ও দামের অনুপাত

মনে করি, ভোক্তা Y দ্রব্য না কিনে ৫ একক X দ্রব্য কিনল। তাতে সে (৫ x ৫ = ২৫) ২৫ টাকা খরচ করে (২৫ +  ২০ + ১৫ + ১০ + ৫ = ৭৫) মোট ৭৫ ইউটিল উপযোগ ভোগ করতে পারবে।

যদি ৪ একক X দ্রব্য এবং ১ একক Y দ্রব্য ক্রয় করে তবে (৪ x ৫ + ১ x ৪ = ২৪) ২৪ টাকায় (২৫ + ২০ + ১৫ + ১০ + ২৪ = ৯৪) মোট ৯৪ ইউটিল উপযোগ ভোগ করতে পারবে।

যদি ৩ একক X এবং ২ একক Y দ্রব্য ক্রয় করে তবে (৩ x  ৫ + ২ x ৪ = ২৩) ২৩ টাকায় ( ২৫ + ২০ + ১৫ + ২৪ + ২০ = ১০৪) মোট ১০৪ ইউটিল উপযোগ ভোগ করতে পারবে।

যদি ২ একক X এবং ৩ একক Y দ্রব্য ক্রয় করে তবে (২*৫ + ৩*৪ = ২২) ২২ টাকায় (২৫+২০+২৪+২০+১৬ = ১০৫) মোট ১০৫ ইউটিল উপযোগ লাভ করতে পারবে।

যদি ১ একক X এবং ৪ একক Y দ্রব্য ক্রয় করে তবে ( ১ x ৫ + ৪ x ৪ = ২১) ২১ টাকায় (২৫ + ২৪ + ২০ + ১৬ + ১২ = ৯৭) মোট ৯৭ ইউটিল উপযোগ লাভ করতে পারবে।

আর যদি শুধু ৫ একক Y দ্রব্য ক্রয় করে তবে, (৫ x ৪ = ২০) ২০ টাকায় (২৪ + ২০ + ১৬ + ১২ + ৮ = ৮০) মোট ৮০ ইউটিল উপযোগ ভোগ করতে পারবে।

উপরের বিশ্লেষণ থেকে দেখা যাচ্ছে সবগুলি সুযোগের মধ্যে ২ একক X এবং ৩ একক Y দ্রব্যের কম্বিনেশনে সর্বোচ্চ উপযোগ লাভ করা সম্ভব।

চিত্রের সাহায্যে সমপ্রান্তিক উপযোগ বিধি ব্যাখ্যা

নিম্নে চিত্রের সাহায্যে সমপ্রান্তিক উপযোগ বিধি ব্যাখ্যা করা হলো-

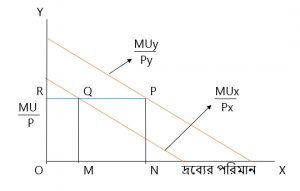
চিত্রঃ  সমপ্রান্তিক উপযোগ রেখা

চিত্রের OX অক্ষে দ্রব্যের পরিমান এবং OY অক্ষে প্রান্তিক উপযোগ ও দামের অনুপাত এবং ব্যয়িত অর্থের প্রান্তিক উপযোগ পরিমাপ করা হয়েছে।

ধরা যাক, অর্থের প্রান্তিক উপযোগ (MUm) = OR।

ভোগকারী OM পরিমান X দ্রব্য এবং ON পরিমান Y দ্রব্য ক্রয় করলে উভয় দ্রব্যের জন্য প্রান্তিক উপযোগ ও দামের অনুপাত MUx/Px ও MUy/Py যথাক্রমে MQ ও NP হবে।

এক্ষেত্রে MQ = NP = OR হওয়াতে ভোগকারী ভারসাম্য লাভ করবে। এ অবস্থায় সে সর্বাধিক উপযোগ পাবে।

সমপ্রান্তিক উপযোগ বিধির সমালোচনা বা দুর্বলতা

দৈনন্দিন জীবনে সমপ্রান্তিক উপযোগ বিধির প্রয়োগগত কার্যকারিতা খুবই সীমাবদ্ধ। তাই অর্থশাস্ত্রের চিরাচরিত নিয়মে অপরাপর বিধির মত সমপ্রান্তিক উপযোগ বিধিও সমালোচনার হাত থেকে রেহাই পায়নি। সমপ্রান্তিক উপযোগ বিধি নিম্নোক্ত সমালোচনার সম্মুখীন হয়েছে।

1. সমপ্রান্তিক উপযোগ বিধিটি মানুষের যুক্তিশীল আচরণের উপর নির্ভরশীল। কিন্তু মানুষ কেনাকাটার সময় সর্বদা যুক্তিনির্ভর আচরণ করে না। মানুষ আবেগ, উত্তেজনা, বিজ্ঞাপনের প্রতারণা, অনুকরণ প্রবৃতির বশে অনেক সময় দ্রব্যের গুনাগুন বিশ্লেষণ না করে ক্রয় করে ফেলে।
2. সমপ্রান্তিক উপযোগ বিধিতে ধরে নেয়া হয়েছে প্রান্তিক উপযোগ পরিমাপের মানদণ্ড অর্থ। এবং আরও ধরা হয়েছে যে, অর্থের প্রান্তিক উপযোগ স্থির। কিন্তু এটা সঠিক নয়। কারণ, বাস্তবে মানুষের আয়ের পরিবর্তনের সাথে সাথে অর্থের প্রান্তিক উপযোগও পরিবর্তিত হয়। তাই অর্থের দ্বারা দ্রব্যের উপযোগ নির্ধারণ সঠিক হয় না।
3. সমপ্রান্তিক উপযোগ বিধিতে ধরে নেয়া হয়েছে উপযোগ পরিমাপ করা যায়। কিন্তু পর্যায়গত উপযোগ ধারণার প্রবক্তারা এর তীব্র প্রতিবাদ জানান। তাদের মতে উপযোগ একটি মনস্তাত্ত্বিক ব্যাপার। তাই এটি পরিমাপ করা সম্ভব নয়।
4. বিভিন্ন প্রকার দ্রব্য কিনে সমপ্রান্তিক উপযোগ পেতে হলে ক্রেতার বাজার সম্পর্কে সুস্পষ্ট ধারণা থাকতে হয়। কিন্তু বাস্তবে সকল ক্রেতার সকল দ্রব্যের দাম বা বাজার সম্পর্কে সমান ধারণা থাকে না।
5. সমপ্রান্তিক উপযোগ বিধিতে ধরে নেয়া হয়েছে যে, সকল দ্রব্যের সতন্ত্র উপযোগ নির্ণয় করা যায়। কিন্তু বাস্তবে এটি সঠিক নয়। কারণ অনেক দ্রব্যের উপযোগ অন্যান্য দ্রব্য ভোগের উপর নির্ভর করতে পারে। যেমন বিদ্যুৎ ব্যহারের উপর বৈদ্যুতিক বাল্বের উপযোগ নির্ভর করে। আবার বিদ্যুতের লোড শেডিং-এর উপর মোমবাতির উপযোগ নির্ভর করে। তাই আলাদাভাবে সব দ্রব্যের উপযোগ নির্ণয় করা সম্ভব নয়।

কাজেই দেখা যাচ্ছে যে, সমপ্রান্তিক উপযোগ বিধির কার্যকারিতা নানাবিধ দিক দিয়ে সীমাবদ্ধ। তবে এটি সম্পূর্ণ অবাস্তব ধারণা নয়। কারণ, মানুষ তার সীমিত অর্থ দিয়ে সর্বাধিক উপযোগ লাভ করতে চায়। তাই মানুষ নিপুণভাবে বিচার বিশ্লেষণ করতে না পারলেও অধিকাংশ ক্ষেত্রে যুক্তিগ্রাহ্য আচরণ করার চেষ্টা করে।

সুতরাং, পরিশেষে আমারা একথা বলতে পারি যে, এতসব সীমাবদ্ধতা থাকা সত্ত্বেও ভোক্তার আচরণ বিশ্লেষণে সমপ্রান্তিক উপযোগ বিধি একটি উন্নততর ধারণা।

সমপ্রান্তিক উপযোগ বিধি থেকে চাহিদা রেখা অংকন

Derivation of Demand Curve from Law of Equi-marginal Utility

সমপ্রান্তিক উপযোগ বিধির সাথে চাহিদা বিধির নিগূঢ় সম্পর্ক রয়েছে। তাই সমপ্রান্তিক উপযোগ বিধি থেকে চাহিদা রেখা অংকন করা যায়।

সমপ্রান্তিক উপযোগ বিধি অনুসারে MUx / Px = MUy / Py = λ।

এখানে, MUx = X পণ্যের প্রান্তিক উপযোগ,

Px = X পণ্যের দাম,

MUy = Y পণ্যের প্রান্তিক উপযোগ,

Py = Y পণ্যের দাম এবং

λ = অর্থের স্থির প্রান্তিক উপযোগ।

ধরি, অন্যান্য সকল অবস্থা অপরিবর্তিত থেকে শুধু X পণ্যের দাম কমল।

Px কমলে MUx/Px বাড়বে। অর্থাৎ, (MUx/Px)¹ > (MUy/Py = λ) হবে। তখন ভোক্তার ভারসাম্য বিঘ্নিত হবে।

ভোক্তার ভারসাম্য পুনরায় ফিরিয়ে আনতে হলে Px যতটুকু কমেছে সে অনুযায়ী MUx কমাতে হবে। MUx কমাতে হলে X পণ্যের ভোগ বাড়াতে হবে।

X পণ্যের ভোগ বাড়ালে MUx কমবে, MUx/Px কমবে।

MUx/Px কমলে (MUx/Px)¹ = MUy / Py = λ হবে। অর্থাৎ আবার ভোক্তার ভারসাম্য স্থাপিত হবে।

অর্থাৎ, সমপ্রান্তিক উপযোগ বিধি থেকে দেখা যাচ্ছে যে, দাম কমলে চাহিদা বৃদ্ধি পায়; যা চাহিদা বিধির প্রতিফলন ঘটায়।

তাই বলা যায় সমপ্রান্তিক উপযোগ বিধি ও চাহিদা বিধি পরস্পর সম্পর্কিত। এজন্য সমপ্রান্তিক উপযোগ বিধি থেকে চাহিদা রেখা অংকন করা যায়।

নিচের চিত্রের সাহায্য তা দেখানো হলো।

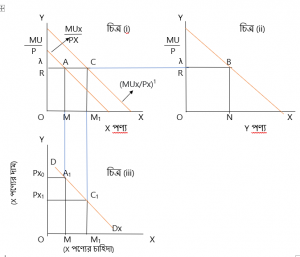
চিত্রঃ  সমপ্রান্তিক উপযোগ বিধি থেকে চাহিদা রেখা অংকন

i নং চিত্রে OX অক্ষে X পণ্য এবং OY অক্ষে MU/P ও অর্থের স্থির প্রান্তিক উপযোগ (λ) ধরা হয়েছে।

MUx/Px হচ্ছে X পণ্যের প্রান্তিক উপযোগ ও দামের অনুপাত রেখা।

ii নং চিত্রে OX অক্ষে Y পণ্য এবং OY অক্ষে MU/P এবং অর্থের স্থির প্রান্তিক উপযোগ (λ) ধরা হয়েছে। MUy/Py হচ্ছে Y পণ্যের প্রান্তিক উপযোগ ও দামের অনুপাত রেখা।

iii নং চিত্রে OX অক্ষে X পণ্যের চাহিদা এবং OY অক্ষে X পণ্যের দাম ধরা হয়েছে। DDx হচ্ছে X পণ্যের চাহিদা রেখা।

প্রাথমিক অবস্থায় ভোক্তা যদি OM পরিমান X পণ্য এবং ON পরিমান Y পণ্য ভোগ করে তাহলে ভোক্তা ভারসাম্য লাভ করবে। কারণ, OR =AM = BN, অর্থাৎ, MUx/Px = MUy/ Py = λ।

এখন, X পণ্যের দাম কমে গেলে MUx/Px রেখা ডানদিকে স্থানান্তরিত হয়ে (MUx/Px)¹ হয়। ফলে ভোক্তার ভারসাম্য বিঘ্নিত হয়।

পুনরায় ভারসাম্যে আসার জন্য ভোক্তা X পণ্যের ভোগ বাড়িয়ে OM₁ করলে C বিন্দুতে (MUx/Px)¹ = CM₁ হয়। ফলে OR = CM₁ = BN অর্থাৎ, (MUx/Px)¹ = MUy/Py = λ হয়। অর্থাৎ, ভোক্তা পুনরায় ভারসাম্য লাভ করে।

তাহলে দেখা যায় যে, X পণ্যের দাম কমার কারণে ভোক্তা ভারসাম্য ঠিক রাখার জন্য X পণ্যের ভোগ বাড়িয়ে দেয়, যা চাহিদা বিধির অনুরূপ।

এখন i নং চিত্র থেকে iii নং চিত্রে X পণ্যের চাহিদা রেখা অংকন করা হয়েছে।

A₁  বিন্দুতে Px₀  দামে X পণ্যের চাহিদা OM । এখন যদি X পণ্যের দাম কমে  Px₁ হয় তা হলে চাহিদার বেড়ে OM₁ হয় যা C₁ বিন্দুতে দেখানো হয়েছে। এখন A₁ ও C₁ বিন্দু যোগ করে যে DDx রেখা পাওয়া যায় উহাই X পণ্যের চাহিদার রেখা।

এভাবে সমপ্রান্তিক উপযোগ বিধি থেকে নিম্নগামী চাহিদার রেখা অংকন করা যায়।